Term rewriting
Table of Contents
Notation
 denotes rewrite rule which rewrites
denotes rewrite rule which rewrites  to
to 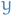 , but not the other way around
, but not the other way around
Preface
- Term rewriting vs. equational logic
- In term rewriting: equations are used as directed replacement rules, i.e. LHS can be replaced by RHS, but not vice versa
- Equational reasoning is concerned with a rather restricted class of first-order languages
- Only predicate symbol is equality
Motivating Examples
- Term rewriting system
- Terms are built up by
- variables
- constant symbols
- function symbols
- Termination: is it always the case that after finitely many rule applications we reach an expression to which no more rules apply?
- The resulting expression is called a normal form
Let  be a term.
be a term.
The normal form of  , denoted
, denoted  , is a term s.t. no further rewrite rules are applicable.
, is a term s.t. no further rewrite rules are applicable.
Symbolic derivation
Consider rules
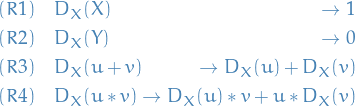
struct Termz{Op} args end struct D var expr end Termz(x) = x Termz(expr::Expr) = begin @assert expr.head === :call Termz{eval(expr.args[1])}(Termz.(expr.args[2:end])) end terms(op, args::AbstractArray) = length(args) > 1 ? Termz{op}(args) : args[1] # Have to implement this explicitly since using different arrays to hold `args` import Base: == ==(t1::Termz{Op1}, t2::Termz{Op2}) where {Op1, Op2} = false ==(t1::Termz{Op}, t2::Termz{Op}) where Op = (t1.args ∩ t2.args) == t1.args t = Termz(:(3x + 2)) D(x, y::Termz) = Termz{D}([x, y]) D(x::Termz, y::Termz) = x == y ? 1 : Termz{D}([x, y]) D(x::Symbol, y::Symbol) = x == y ? 1 : 0 D(x, y::Number) = 0 D(x, t::Termz{+}) = begin # @info "calling Termz{+} with args" t Termz{+}(D.(x, t.args)) end D(x, t::Termz{*}) = begin # @info "calling Termz{*} with args" t Termz{+}([ Termz{*}([ D(x, t.args[1]), t.args[2:end]... ]), Termz{*}([ t.args[1], D(x, terms(*, t.args[2:end])) ]) ]) end D(x, t::Termz{^}) = begin # @info "calling Termz{^} with args" t Termz{*}([ t.args[end], # exponent Termz{^}([ t.args[1], Termz{+}([t.args[end], -1]) ]) ]) end eval(x::Number) = x eval(x::Number, dict) = x eval(x::Symbol, dict) = dict[x] eval(t::Termz{Op}) where Op = foldl(Op, eval.(t.args)) eval(t::Termz{Op}, dict) where Op = foldl(Op, [eval(a, dict) for a ∈ t.args]) (t::Termz)(; kwargs...) = eval(t, kwargs) function variables(t::Termz; res = Set()) for t_ ∈ t.args if t_ isa Symbol push!(res, t_) elseif t_ isa Termz variables(t_; res = res) end end return res end "Generates an anonymous function which evaluates together with the variable ordering." generate(t::Termz) = begin vars = collect(variables(t)) if length(vars) == 0 return () -> eval(t, Dict()), [] end expr = quote ($(vars...)) -> eval(t, Dict(zip($vars, [$(vars...)]))) end return eval(expr), vars end # TESTING eval(D(:x, t), Dict(:x => 2.0)) eval(t, Dict(:x => 1.0)) der = D(:x, Termz(:(3 * x * y))) der(; x = 0.0, y = 1.0) # Addition t = Termz(:(x + 1)) @assert t(; x = 1) == 2 @assert D(:x, t)(; x = 100) == 1 # Multiplication t = Termz(:(x * y)) @assert t(; x = 1.0, y = 2.0) == 2.0 @assert D(:x, t)(; x = 1.0, y = 2.0) == 2.0 # Power t = Termz(:(x^3)) @assert t(; x = 2.0) == 8.0 @assert D(:x, t)(; x = 2.0) == 12.0 # All combined t = Termz(:((3 + x)x^2 + 2x + 1)) @assert t(; x = 1) == 7 @assert D(:x, t)(; x = 2) == 26 println(D(:x, t)) println(D(:x, t)(; x = 2)) println(D(:x, Termz(:(x * x)))) # Macros for convenience macro termz(expr) Termz(expr) end macro D(var, expr) D(Termz(var), Termz(expr)) end println() println("Macros:") println(@termz 1 + x) println(@D(x, 1 + 100x)) println(@D(x, x * x)) println(@D(x, f(x))) println(D(:x, @termz f(x))) println(@D(f(x), f(x))) # println(@D(g(x), f(x))) # FIXME: currently requires the function to be defined g() = 1 # but doesn't have to have the correct signature; though `eval` will fail println(@D(g(x), f(x)))
Termz{+}(Any[Termz{+}(Termz{*}[Termz{*}(Termz[Termz{+}([0, 1]), Termz{^}(Any[:x, 2])]), Termz{*}(Termz[Termz{+}(Any[3, :x]), Termz{*}(Any[2, Termz{^}(Any[:x, Termz{+}([2, -1])])])])]), Termz{+}(Termz{*}[Termz{*}(Any[0, :x]), Termz{*}([2, 1])]), 0])
26
Termz{+}(Termz{*}[Termz{*}(Any[1, :x]), Termz{*}(Any[:x, 1])])
Macros:
Termz{+}(Any[1, :x])
Termz{+}(Any[0, Termz{+}(Termz{*}[Termz{*}(Any[0, :x]), Termz{*}([100, 1])])])
Termz{+}(Termz{*}[Termz{*}(Any[1, :x]), Termz{*}(Any[:x, 1])])
Termz{D}(Any[:x, Termz{f}(Symbol[:x])])
Termz{D}(Any[:x, Termz{f}(Symbol[:x])])
1
Termz{D}(Termz[Termz{g}(Symbol[:x]), Termz{f}(Symbol[:x])])
By applying the corresponding rules in sequence we get
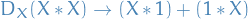
- Confluence
- Say there are different ways of applying rules to a given term

- Suppose these different ways lead to two different terms
 and
and 
- Can we always find a common term
 that can be reached from both
that can be reached from both  and
and  by application of the defined rules?
by application of the defined rules? - If this is true (for all terms in this system), we have confluence for the defined rules
- Say there are different ways of applying rules to a given term
- Completion
- Can we always make a non-confluent system into a confluent system by adding implied rules
- This is referred to as completion of the system
One can show that  is actually confluent.
is actually confluent.
- Suppose we have some arbitrary term

- Consider all possible rules that was applied to the previous term

OR
- All rules are independent
- Rules
 constitutes a functional program
constitutes a functional program
- On the LHS, the defined function
 occurs only at the very outside
occurs only at the very outside
- On the LHS, the defined function
- Termination of the resul means that $DX is a total function
- Confluence of the rules means that the result of a computation is independent of the evaluation/rewrite strategy
All term rewriting systems that constitute functional programs are confluent.
Group Theory
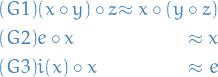
Given a set of identities  and two terms
and two terms  and
and  , is it possible to transform the term
, is it possible to transform the term  into the term
into the term  , using the identities in
, using the identities in  as rewrite rules that can be applied in both directions?
as rewrite rules that can be applied in both directions?
There are a couple of problems we need to overcome:
- Equivalent terms can have distinct normal forms
- Normal forms need not exist
Abstract reduction system
An abstract reduction system is a pair 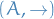 , where the reduction
, where the reduction  is a binary relation on the set
is a binary relation on the set 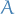 , i.e.
, i.e. 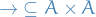 .
.
Instead of  we write
we write  ..
..
So a binary relation is just a subset of  which satisfy some property.
which satisfy some property.
Notation
Identity:

(i + 1)-fold composition,


Transistive closure
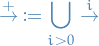
Reflexive transistive closure

Reflexive closure

Inverse

Inverse

Symmetric closure

Transistive symmetric closure
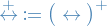
Reflexive transistive symmetric closure

 is reducible if and only if
is reducible if and only if
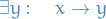
 is in normal form (irreducible) if and only if it is not reducible
is in normal form (irreducible) if and only if it is not reducible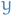 is a normal form of
is a normal form of  if and only if
if and only if  and
and 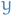 is in normal form. If
is in normal form. If  has a uniquely determined normal form, the latter is denoted by
has a uniquely determined normal form, the latter is denoted by  .
.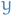 is a direct successor of
is a direct successor of  if and only if
if and only if 
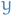 is a successor of
is a successor of  if and only if
if and only if 
 and
and 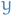 are joinable if and only if
are joinable if and only if

in which case we write

A reduction
 is called Church-Rosser if and only if
is called Church-Rosser if and only if
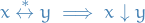
A reduction
 is called confluent if and only if
is called confluent if and only if

- A reduction
 is called terminating if and only if there is no infinitiely descending chain
is called terminating if and only if there is no infinitiely descending chain 
- A reduction
 is called normalizing if and only if every element has a normal form
is called normalizing if and only if every element has a normal form - A reduction
 is called convergent if and only if it is both confluent and terminating
is called convergent if and only if it is both confluent and terminating
Equivalence and reduction
Can view reduction in two ways
- Directed computation, starting from some point
 , and then tries to reac a normal form by following the reduction
, and then tries to reac a normal form by following the reduction 
- Corresponds to idea of program evaluation
- Consider
 merely as a description of
merely as a description of  , where
, where  means that there is a path between
means that there is a path between  and
and  where the arrows can be traversed in both directions, e.g.
where the arrows can be traversed in both directions, e.g. 
- Corresponds to idea of identities which can be used in both directions
So
- (2) is of course very slow to do in general, so would be nice if we could do (1) until we reach normal form and then compare the normal forms of the expressions
- Only works if reduction terminates and normal forms are unique: formally, we need termination and confluence of reduction
Basic definitions
- Two relations
 and
and 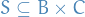
Their composition is defined by


- Notations like
 and
and  only work for arrow-like symbols
only work for arrow-like symbols
- In the case of arbitrary relations
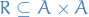 we write
we write 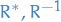 , etc.
, etc.
- In the case of arbitrary relations
- Some of the constructions can also be expressed nicely in terms of paths:
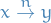 if there is a path of length
if there is a path of length  from
from  to
to 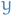
 if there is some finite path from
if there is some finite path from  to
to 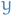
 if there is some finite nonempty path from
if there is some finite nonempty path from  to
to 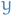
- The
 of
of  is the least set with property
is the least set with property  which contains
which contains 
- E.g.
 , the reflexive transistive closure of
, the reflexive transistive closure of  , is the least reflexive and transisitve relation which contains
, is the least reflexive and transisitve relation which contains  .
. - For arbitrary
 and
and  , the
, the  of
of  need not exist, but in the above cases they always do because reflexivity, transistivity and symmetry are closed under arbitrary intersections
need not exist, but in the above cases they always do because reflexivity, transistivity and symmetry are closed under arbitrary intersections
- In such cases, the
 can be be defined directly as the intersection of all sets with property
can be be defined directly as the intersection of all sets with property  which contain
which contain 
- In such cases, the
- E.g.
- Claim:
 is the least equivalence relation containing
is the least equivalence relation containing 
- Proof: An equivalence relation containing
 must also contain
must also contain  by the symmetry property of a equivalence relation, thus is contains
by the symmetry property of a equivalence relation, thus is contains  . We just need to verify that it also contains
. We just need to verify that it also contains  and any number of
and any number of  . Observe first that
. Observe first that  is definitively in it because of the reflexitivity of the equivalence relation. Finally it then contains
is definitively in it because of the reflexitivity of the equivalence relation. Finally it then contains  because of transistivity. Hence any other equivalence relation
because of transistivity. Hence any other equivalence relation  containing
containing  must contain
must contain  (set corresponding to
(set corresponding to  ), i.e. it's the least equivalence relation containing
), i.e. it's the least equivalence relation containing  .
.
- Proof: An equivalence relation containing
Sudoku solver
- Why? Because we can
cell_candidates(i, j, grid) = [k for k = 1:size(grid, 1) if k ∉ (Set(grid[i, :]) ∪ Set(grid[:, j]))] subsolve!(grid) = begin # solve all the straight forward ones for i = 1:size(grid, 1) for j = 1:size(grid, 2) if grid[i, j] == 0 candidates = cell_candidates(i, j, grid) if length(candidates) == 1 grid[i, j] = candidates[1] end end end end grid end solve!(grid; level = 0) = begin @info level success = false prev_soln = zeros(size(grid)) num_steps = 0 while grid != prev_soln copy!(prev_soln, grid) subsolve!(grid) # increment step counter num_steps += 1 # @info "Completed step $num_steps" end # at this point, we either solved it completely or there are ambigious entries unsolved = findall(zeros(size(grid)) .== grid) # @info "unsolved" unsolved issolved = length(unsolved) == 0 if !issolved # try out filling in different entries; starting with the ones with the fewest # possible candidates unsolved_ns = [length(cell_candidates(idx[1], idx[2], grid)) for idx ∈ unsolved] if 0 ∈ unsolved_ns return false end unsolved_indices = sort(1:length(unsolved); by = i -> unsolved_ns[i]) # @info unsolved_ns[unsolved_indices] for i ∈ unsolved_indices idx = unsolved[i] soln = copy(grid) for v ∈ cell_candidates(idx[1], idx[2], soln) soln[idx] = v issolved = solve!(soln; level = level + 1) issolved && @info soln if issolved grid .= soln return true end end # @info "failed to solve grid" end end unsolved = findall(zeros(size(grid)) .== grid) return length(unsolved) == 0 # issolved end solve(grid) = begin soln = copy(grid) issolved = solve!(soln) if !issolved @warn "failed to solve Sudoku" end return soln end # # simple case # grid = [ # 0 1 3; # 3 2 0; # 0 0 2 # ] # @assert solve(grid) == [2 1 3; 3 2 1; 1 3 2] # grid = [ # 0 1 3 0 5; # 3 2 0 0 0; # 0 0 2 0 0; # 4 0 0 3 0; # 1 0 0 0 0 # ] # solve(grid) # FAILED!!! # Takes forever to run; might be a mistake in the grid grid = [ 5 3 0 0 7 0 0 0 0; 6 0 0 1 9 6 0 0 0; 0 9 8 0 0 0 0 6 0; 8 0 0 0 6 0 0 0 3; 4 0 0 8 0 3 0 0 1; 7 0 0 0 2 0 0 0 6; 0 6 0 0 0 0 2 8 0; 0 0 0 4 1 9 0 0 5; 0 0 0 0 8 0 0 7 9; ] size(grid) @time res = solve(grid) # Solved ✓ # - Requires 1 lvl nesting grid = [ 0 0 3 0 1 0; 5 6 0 3 2 0; 0 5 4 2 0 3; 2 0 6 4 5 0; 0 1 2 0 4 5; 0 4 0 1 0 0; ] # Solved ✓ # - Requires 4 lvl nesting grid = [ 0 0 0 1 0 6; 6 0 4 0 0 0; 1 0 2 0 0 0; 0 0 0 5 0 1; 0 0 0 6 0 3; 5 0 6 0 0 0; ] # Solved ✓ # - Requires 14 lvl nesting grid = [ 0 0 0 4 0 0; 0 0 6 0 0 3; 0 0 0 0 0 0; 0 0 0 0 0 0; 6 0 0 5 0 0; 0 0 1 0 0 0 ] # 7 x 7 # Solved ✓ # - Requires 17 lvl nesting grid = [ 0 4 0 0 3 1 6 0; 1 0 0 0 0 0 0 0; 8 0 0 0 0 0 0 0; 4 3 0 0 2 0 0 0; 0 0 0 8 0 0 3 4; 0 0 0 0 0 0 0 5; 0 0 0 0 0 0 0 6; 0 7 4 5 0 0 8 0; ] # 8 x 8 # Solved ✓ # - Requires 10 lvl nesting grid = [ 0 0 0 0 7 0 0 6; 0 0 0 5 3 0 0 7; 0 0 0 0 0 6 1 0; 3 0 2 0 0 5 0 0; 0 0 0 0 0 0 0 1; 8 4 0 0 0 0 0 0; 0 0 8 0 0 2 0 0; 0 6 0 1 5 0 0 0 ] # Solved ✓ # - Requires lvl 14 nesting grid = [ 0 0 0 2 0 3 0 0; 0 0 6 0 0 7 0 0; 3 8 0 0 0 0 6 0; 0 0 0 7 3 0 0 5; 7 0 0 4 1 0 0 0; 0 2 0 0 0 0 7 4; 0 0 3 0 0 5 0 0; 0 0 1 0 7 0 0 0; ] @assert size(grid) == (8, 8) # 9 x 9 # Solved ✓ # - Requires lvl 14 nesting # - @time: 1.177324 seconds (16.63 M allocations: 1.678 GiB, 17.42% gc time) grid = [ 5 3 0 0 7 0 0 0 0; 6 0 0 1 9 5 0 0 0; 0 9 8 0 0 0 0 6 0; 8 0 0 0 6 0 0 0 3; 4 0 0 8 0 3 0 0 1; 7 0 0 0 2 0 0 0 6; 0 6 0 0 0 0 2 8 0; 0 0 0 4 1 9 0 0 5; 0 0 0 0 8 0 0 7 9 ] # Solved ✓ # - Requires lvl 18 nesting # - @time: 0.020624 seconds (285.23 k allocations: 28.252 MiB, 11.97% gc time) grid = [ 0 0 0 1 0 5 0 6 8; 0 0 0 0 0 0 7 0 1; 9 0 1 0 0 0 0 3 0; 0 0 7 0 2 6 0 0 0; 5 0 0 0 0 0 0 0 3; 0 0 0 8 7 0 4 0 0; 0 3 0 0 0 0 8 0 5; 1 0 5 0 0 0 0 0 0; 7 9 0 4 0 1 0 0 0; ] # Solved ✓ # - Requires lvl 39 nesting # - @time: 0.036620 seconds (693.66 k allocations: 68.903 MiB, 16.69% gc time) grid = [ 1 0 0 0 0 0 0 0 0; 0 0 0 0 1 2 0 0 0; 0 0 0 0 0 0 0 0 1; 0 8 0 0 0 0 5 0 1; 0 5 0 0 8 9 0 0 7; 0 9 0 0 0 0 0 0 0; 0 0 0 0 0 0 6 5 0; 0 0 0 0 0 0 0 0 0; 0 0 0 0 3 0 0 0 0; ] # Solved ✓ # - Requires 2 lvl nesting # - @time: 0.011032 seconds (160.33 k allocations: 16.076 MiB, 20.82% gc time) grid = [ 0 0 9 0 7 0 4 3 6; 0 0 0 3 8 0 9 0 0; 6 3 2 5 0 0 0 0 0; 7 6 3 8 0 0 0 4 0; 4 0 0 1 0 7 0 0 8; 0 2 0 0 0 3 5 6 7; 0 0 0 0 0 8 2 7 3; 0 0 6 0 3 9 0 0 0; 3 5 8 0 1 0 6 0 0; ] @assert size(grid) == (9, 9) @time res = solve(grid) res